The cursor will change its shape to a small right-pointing arrow for rows and to a small downward-pointing arrow for columns.
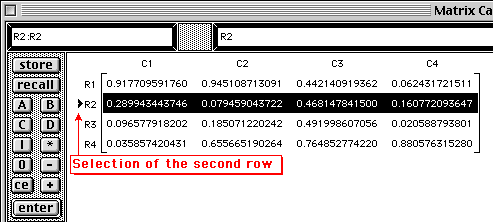
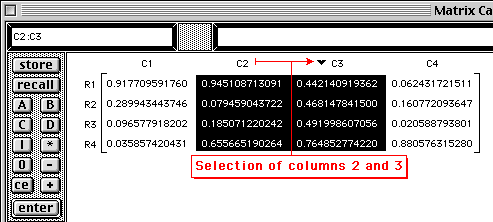
The cursor will change its shape to a small right-pointing arrow for rows and to a small downward-pointing arrow for columns.


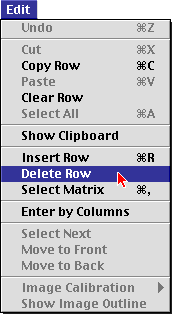
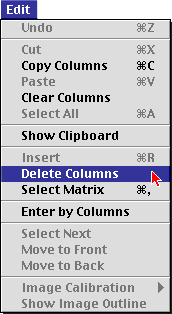
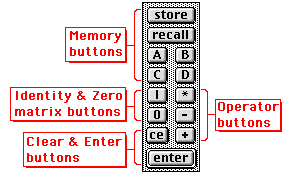
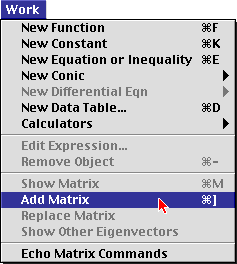
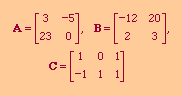
|
|
Warning: Here "Enter" means to press the Enter key and not the Return key!. |
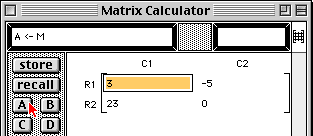
|
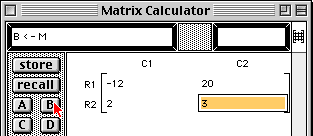
4A - 3/2 B |
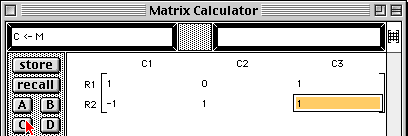
|
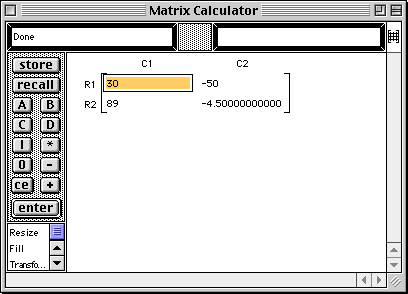
5A - 4I + B |
|
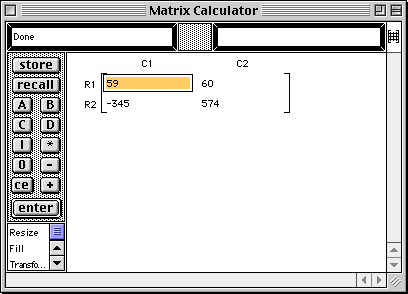
ABC |
|
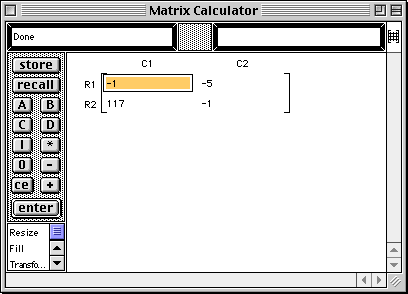
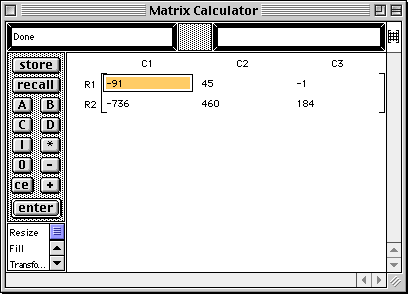
A(B - A) - I |
You must compute B - A first and store it since matrix multiplication is not commutative.
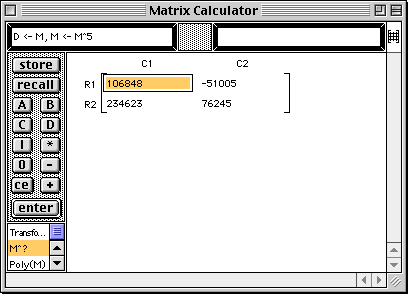
![]()

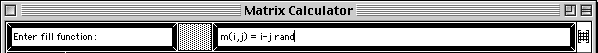
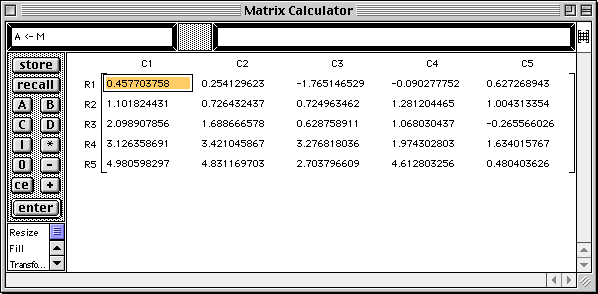
Note that the value of the determinant is written into the command area of the Matrix Calculator window.
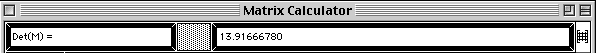
The value of ![]() is
written into the command area.
is
written into the command area.
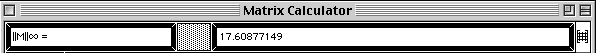
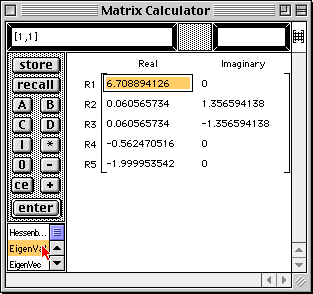
The eigenvalues are written into the matrix area of the Matrix Calculator window.
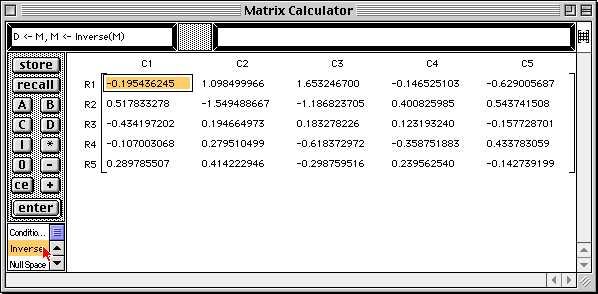
The inverse matrix is written into the matrix area of the Matrix Calculator window.
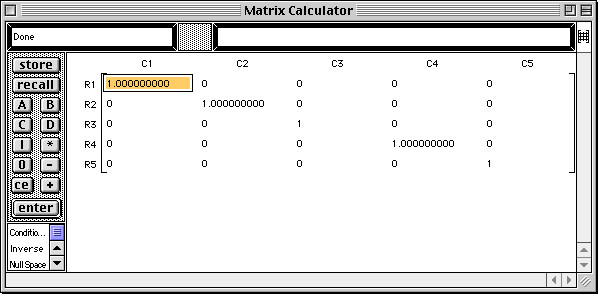
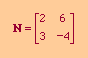
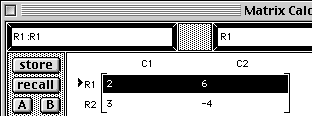
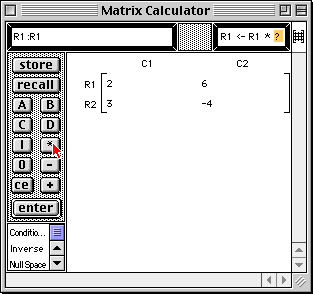
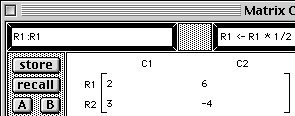
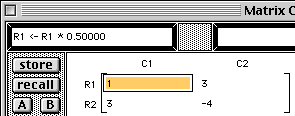
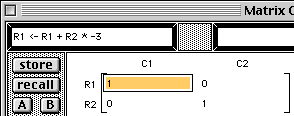
The template "R2 <- R2 + R? * ?" is written into the command area.
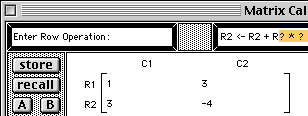
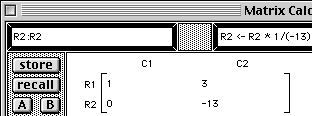
You also could have simply edited the template to read "R2 <- R2 + R1 * (-3)". The parentheses around the -3 are necessary, otherwise, you would have two arithmetic operators next to each other *-.



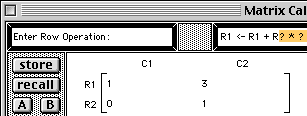
The template "R1 <- R1 + R? * ?" is written into the command area.
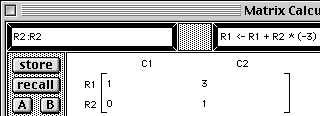
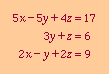
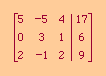
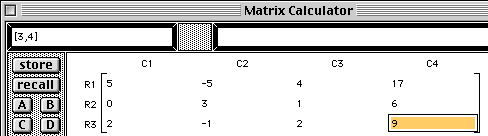
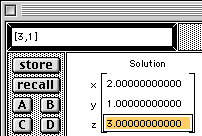
|
Copyright 2000-2008 Adam O. Hausknecht and Robert E. Kowalczyk